Optische Linsen - Bildkonstruktion und Berechnungen
Auf unserer Seite über Strahlenoptik (auch als geometrische Optik bezeichnet) haben wir im Kapitel Brechung von Lichtstrahlen gezeigt, wie Lichtstrahlen abgelenkt werden, wenn sie von einem Medium wie Luft in ein anderes, z.B. Glas, gelangen. Im praktischen Teil des Kapitels haben wir gezeigt, wie man den Effekt der Lichtbrechung in der Praxis nutzt, zum Beispiel in Umkehrprismen oder in Lichtwellenleitern.
Die größte Anwendung der Lichtbrechung kommt jedoch beim Einsatz von Linsen in der fotografischen Optik vor. Es gibt unzählige Linsenformen und Linsenarten, die Licht auf unterschiedlichste Art brechen. Auf dieser Seite zeigen wir Ihnen, wie Konvex- und Konkavlinsen Licht brechen, wie man das Bild eines Gegenstandes bei der Abbildung an einer Linse konstruiert, wie sich der Abbildungsmaßstab ergibt und wie man die Brennweite und den Brechwert einer Linse berechnet.
Sphärische Linsen, Linsenformen
Optische Linsen sind zumeist sphärischer Natur, d.h. ihre Begrenzungsflächen sind Teile von Kugelflächen. Der Begriff sphärisch leitet sich aus dem griechischen Wort sphaira für Ball ab. Linsen bestehen entweder aus Glas, aus Kunststoff oder aus anderen durchsichtigen Materialien wie Kristallen; Glaslinsen kommen bei vielen Anwendungen wegen ihres hohen Gewichtes nicht in Frage.
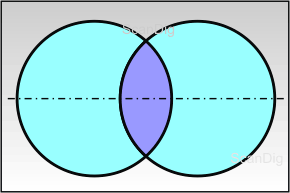
Wie sieht eine optische Linse aus, deren Begrenzungsflächen Teile von Kugelflächen sind? Beim Begriff Kugel stellt man sich immer gleich einen runden Ball oder eine halbe Kugel bzw. eine Schale vor. Macht man jedoch einen Schnitt an einer Kugel, so entsteht je nach Schnitttiefe eine leicht oder stark gewölbte Kugeloberfläche mit einer platten Schnittseite. Die nebenstehende Abbildung zeigt, wie eine doppelt gewölbte (bikonvexe) Linse als Schnitt aus zwei Kugelflächen entsteht: Die Bikonvexlinse ergibt sich aus den beiden Kugelteilflächen bis zu ihrem Schnittpunkt oben und unten; die hellen Bereiche der beiden Kugeln schneidet man weg. Verbindet man die Mittelpunkte der beiden Kugeln mit einer gestrichelten Linie so ergibt sich die optische Achse der entstehenden Linse. Entsprechend dem obigen Bild entstehen andere Linsenarten (siehe im folgenden) durch Schnitte von Außenkugelflächen, Innenkugelflächen und planen Flächen.
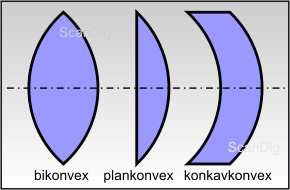
Bei optischen Linsen führt man eine grundlegende Unterscheidung zwischen Sammellinsen und Zerstreuungslinsen durch. Sammellinsen werden auch als Konvexlinsen, Zerstreuungslinsen auch als Konkavlinsen bezeichnet. Eine nach außen gewölbte Linsenoberfläche wird als konvex bezeichnet, eine flache Linsenoberfläche wird als plan bezeichnet, und eine nach innen gewölbte Oberfläche wird als konkav bezeichnet.
Abbildung 2 zeigt unterschiedliche Varianten von Konvexlinsen, die jeweils auf einer gemeinsamen optischen Achse angeordnet sind. Eine auf beiden Seiten nach außen gewölbte Linse, die innen also dicker ist als am Rand, wird als Binkonvexlinse bezeichnet. Dabei muss die Linse nicht symmetrisch sein, d.h. die beiden Linsenaußenflächen können unterschiedlich stark gewölbt sein. Ist eine Seite der Linse flach und eine nach außen gewölbt, so wird die Linse als plankonvex bezeichnet. Ist die linke Seite nach innen und die rechte Seite nach außen gewölbt so handelt es sich um eine konkavkonvexe Linse. In der Optik werden solche konkavkonvexe bzw. konvexkonkave Linsen auch als Meniskus bezeichnet. Ein positiver bzw. negativer Meniskus zeichnet sich also dadurch aus, dass sich beide Linsenflächen zur gleichen Seite hin neigen.
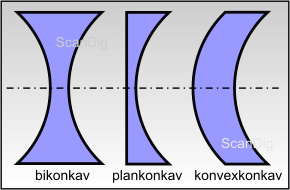
Abbildung 3 zeigt unterschiedliche Konkavlinsen: Sind beide Seiten einer optischen Linse nach innen gewölbt, ist die Linse in der Mitte also dünner als am oberen und unteren Rand, so wird die Linse als bikonkav bezeichnet. Die beiden Linsenoberflächen dürfen unterschiedliche Krümmungsradien haben, d.h. die Linse muss nicht symmetrisch sein. Ist eine Seite flach und nur eine Seite nach innen gewölbt spricht man von einer plankonkaven Linse. Entsprechend gibt es eine konvexkonkave Linse, wenn eine Seite nach außen und eine nach innen gewölbt ist.
Sphärische Linsen sind in der Produktion einfach herzustellen, da die Linsenoberflächen Teile von Kugelflächen sind und somit einen festen Radius haben. Da sphärische Linsen jedoch sogenannte sphärische Abbildungsfehler aufweisen werden bei hochwertigen optischen Geräten wie zum Beispiel teuren Objektiven asphärische Linsen eingesetzt, deren Oberfläche nicht mehr kugelförmig sondern zum Beispiel parabolförmig ist. Mit asphärischen Linsen lassen sich bessere optische Eigenschaften erzielen, jedoch ist der Preis von asphärischen Linsen um ein Vielfaches höher wegen der aufwändigen und komplizierten Produktion.
Brechung von Lichtstrahlen an dünnen Linsen
Auf unserer Seite über Strahlenoptik haben wir im Kapitel Brechung gelernt, dass Lichtstrahlen beim Übergang von optisch unterschiedlich dichten Medien gebrochen werden. Optisch unterschiedlich dichte Medien sind zum Beispiel Luft und Glas. Beim Übergang von Luft in Glas wird ein Lichtstrahl zum Einfallslot hingebrochen, da Glas das optisch dichtere Medium ist. Andersherum wird beim Übergang von Glas in Luft ein Lichtstrahl vom Einfallslot weggebrochen. Wir haben uns diesen zweifachen Brechungseffekt an unterschiedlichen Prismen veranschaulicht und gelernt, dass deswegen ein Lichtstrahl durch Prismen umgelenkt werden kann.
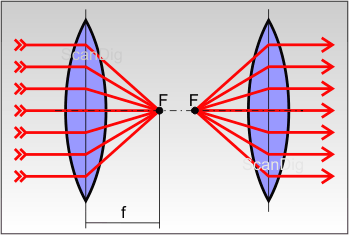
Wenn ein Lichtstrahl beim Übergang von Luft in Glas und umgekehrt gebrochen, also abgelenkt, wird, dann gilt dies selbstverständlich auch für Lichtstrahlen, die auf eine optische Linse treffen. Betrachten wir zunächst die Bikonvexlinse (linker Teil) in Abbildung 4. Treffen auf eine solche Linse von links zur optischen Achse parallele Lichtstrahlen, wie sie zum Beispiel von der Sonne oder einem weit entfernten Gegenstand herkommen, ein, so wird jeder einzelne Lichtstrahl derart gebrochen, dass er auf den sogenannten Brennpunkt trifft. Derjenige Lichtstrahl, der entlang der optischen Achse auf die Linse trifft wird nicht abgelenkt, da er ja jeweils mit einem Winkel von 90° in die Linse eintritt und wieder austritt. Je weiter außen die Lichtstrahlen auf die Linse treffen desto größer ist die Ablenkung durch die Linse. Da alle Parallelstrahlen im Brennpunkt der Linse gesammelt werden spricht man bei solchen Linsen auch von Sammellinsen. Der Abstand des Brennpunktes F von der Linsenmitte bezeichnet man als Brennweite f der Linse. Halten wir dies fest:
Bei Sammellinsen werden Parallelstrahlen im Brennpunkt F hinter der Linse gebündelt. Der Abstand zwischen Linsenmittelpunkt und Brennpunkt wird als Brennweite bezeichnet.
Eine typische Anwendung für eine bikonvexe Linse ist eine Leselupe. Mit einer Lupe kann man Lichtstrahlen, die von der Sonne oder von einer Zimmerlampe kommen, so bündeln, dass im Brennpunkt ein heller bzw. heißer Fleck entsteht. Damit erhält der Name Brennpunkt auch eine anschauliche Erklärung.
Betrachten wir nun den rechten Teil von Abbildung 4: Hier wird eine Lichtquelle genau im Brennpunkt der Sammellinse aufgestellt. Diejenigen Lichtstrahlen, die vom Brennpunkt aus auf die Linse treffen, werden in achsenparallele Strahlen umgelenkt. Derjenige Lichtstrahl, der vom Brennpunkt aus entlang der optischen Achse verläuft, durchdringt die Linse ungestört. Während bei einer Bikonvexlinse Achsenparallelstrahlen also im Brennpunkt gesammelt werden, werden Lichstrahlen vom Brennpunkt ausgehend in achsenparalelle Strahlen umgelenkt.
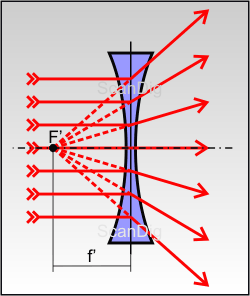
Wie werden Lichtstrahlen von einer Konkavlinse gebrochen? Betrachten wir dazu die Abbildung 5: Parallelstrahlen, also Lichtstrahlen, die parallel zur optischen Achse auf die Linse einfallen, werden von der Linse weggebrochen. Nur derjenige Lichtstrahl, der entlang der optischen Achse auf die Linse einfällt, wird von der Konkavlinse nicht abgelenkt, da er jeweils mit einem Winkel von 90° in die Glasoberfläche eintritt bzw. wieder austritt. Alle anderen Parallelstrahlen werden von der Linse weggebrochen als kämen sie von einem vor der Linse liegenden Brennpunkt F'. Es handelt sich um einen scheinbaren, virtuellen Brennpunkt; daher sind die scheinbaren Strahlen in der Zeichnung gestrichelt eingezeichnet. Die Bikonkavlinse zerstreut also die parallel eintreffenden Lichtstrahlen, weshalb eine solche Linse auch als Zerstreuungslinse bezeichnet wird. Auch bei einer Zerstreuungslinse wird als Brennweite f der Abstand vom Linsenmittelpunkt zum Brennpunkt F' bezeichnet. Da es sich um einen virtuellen Brennpunkt handelt, der auf der Gegenstandsseite liegt, wird die Brennweite oft mit einem negativen Zahlenwert angegeben. Halten wir auch die wichtige Eigenschaft einer Bikonkavlinse fest:
Bei Zerstreuungslinsen werden parallele Lichstrahlen so zerstreut als kämen sie von einem Brennpunkt F', der vor der Linse liegt und deshalb als virtueller Brennpunkt bezeichnet wird.
Beim Vergleich der Eigenschaften von Sammellinsen und Zerstreuungslinsen wird schnell klar, dass in technischen Anwendungen meist Sammellinsen zum Einsatz kommen, um Licht zu sammeln und zu bündeln. Der bloße Einsatz von Zerstreuungslinsen macht in der Praxis wenig Sinn; Zerstreuungslinsen kommen meist im Zusammenspiel mit Sammellinsen zum Einsatz.
Vereinfachung für dünne Linsen: In den obigen Zeichnungen haben wir die Brechung der Lichtstrahlen so veranschaulicht, als würde die Brechung in der Linsenmitte stattfinden. Tatsächlich findet beim Durchgang eines Lichtstrahles durch eine Linse jedoch eine zweimalige Brechung des Lichtes, nämlich beim Eintritt in die Linse und beim Austritt aus der Linse, statt. Im Innern der Linse breitet sich Licht wieder geradlinig fort. Eine derartige Lichtausbreitung betrachten wir später im Kapitel Dicke Linsen genauer. Solange wir uns auf dünne Linsen beschränken können wir mit dieser Vereinfachung arbeiten. Die Brechung der Lichtstrahlen wird dann wie in den Abbildungen gezeigt in der Linsenmitte angenommen; die senkrecht zur optischen Achse stehende Ebene wird als Hauptebene der Linse bezeichnet.
Konstruktion des Linsenbildes bei dünnen Linsen
Im vorigen Kapitel haben wir gelernt wie Lichtstrahlen an einer dünnen Konvexlinse oder Konkavlinse gebrochen werden. Dabei war die Kernaussage, dass Parallelstrahlen bei einer Konvexlinse im Brennpunkt F gebündelt werden, bei einer Konkavlinse jedoch zerstreut werden mit einem virtuellen Brennpunkt F' als Zerstreuungs-Ausgangspunkt. In diesem Kapitel geht es darum, wie man mit Hilfe von charakteristischen Lichstrahlen das Bild eines Gegenstandes konstruiert, dessen Licht durch eine Konvexlinse oder Konkavlinse dringt.
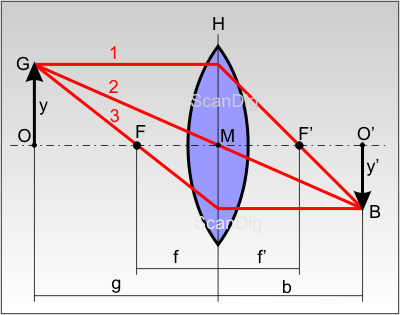
Beginnen wir mit der Bildkonstruktion an einer Bikonvexlinse, wie sie in Abbildung 6 gezeigt ist. Der Linsenmittelpunkt ist mit M eingezeichnet, die senkrechte Schnittebene durch die Linse wird als Hauptebene H bezeichnet. Senkrecht dazu stellt die strichpunktierte Linie die optische Achse der Linse dar. Auf ihr liegt links der Linse der gegenstandseitige Brennpunkt F, rechts der Linse befindet sich der bildpunktseitige Brennpunkt F'. Die zugehörigen Brennweiten sind mit f und f' bezeichnet. Bei einer symmetrischen Linse ist f=f'. Uns interessiert nun, wie der Gegenstand G durch die Linse abgebildet wird. Beim Gegenstand G handelt es sich um einen einfachen Pfeil, dessen Ursprung O auf der optischen Achse liegt; der Punkt G wird als Gegenstandspunkt G bezeichnet. Die Höhe des abzubildenden Gegenstandes ist mit y eingezeichnet und hat die Bezeichnung Gegenstandsgröße y. Der gesamte Bildbereich links der Linse wird auch als Gegenstandsraum bezeichnet. Um das Bild des Pfeiles zwischen O und G zu konstruieren genügt es, das Bild der beiden Punkte O und G zu finden.
Beginnen wir mit der Abbildung des Gegenstandspunktes G. Dazu betrachten wir drei charakteristische Lichtstrahlen, die vom Punkt G in Richtung Linse verlaufen. In der Abbildung ist der obere Strahl 1 ein Parallelstrahl, der, wie wir im vorigen Kapitel gelernt haben, durch die Linse so gebrochen wird, dass er durch den bildseitigen Brennpunkt F' verläuft. Der Strahl 2 wird als Mittelpunktstrahl bezeichnet; er verläuft durch den Linsenmittelpunkt hindurch und wird nicht abgelenkt. Der Strahl 3 wird als Brennpunktstrahl bezeichnet; er durchkreuzt den gegenstandsseitigen Brennpunkt und wird dann von der Linse zu einem Parallelstrahl abgelenkt. Diese drei charakteristischen Lichtstrahlen treffen sich im Bildpunkt B auf der Bildseite rechts im Bild. Zur Konstruktion dieses Bildpunktes reichen zwei solcher Hauptstrahlen aus. Damit steht der zum Gegenstandspunkt G gehörige Bildpunkt B fest. Der Ursprung O des Gegenstandes auf der optischen Achse wird in den Punkt O' abgebildet. Diesen Punkt brauchen wir nicht extra zu konstruieren, denn wir wissen, dass er auf der optischen Achse liegen und senkrecht zum Bildpunkt B verlaufen muss. Aus den Punkten O' und B ergibt sich auch die Bildgröße y'.
Aus der obigen Zeichnung erkennen wir sofort, dass unser Gegenstand G durch die Abbildung der Linse auf den Kopf gestellt wird. Auch erkennen wir, dass die Bildgröße y' kleiner als die Gegenstandsgröße y ist; die Bikonvexlinse führt also in diesem Beispiel zu einer Verkleinerung des Gegenstandes auf der Bildseite. Bevor wir zur Bildgröße ins Detail gehen halten wir zunächst fest:
Bei dünnen Konexlinsen konstruiert man das Linsenbild mit Hilfe von 2 der 3 Hauptstrahlen Parallelstrahl, Mittelpunktstrahl oder Brennpunktstrahl. Man erhält ein kopfstehendes Bild B des Gegenstandes G.
Dass die Verkleinerung des Gegenstandes bei der Abbildung mittels einer Bikonvexlinse nur einer von mehreren Fällen ist zeigen wir im Folgenden mit Hilfe der Abbildung 7. Darin ist die gleiche Linse wie im vorigen Beispiel dargestellt. Abgebildet werden 4 gleich große Gegenstände G1, G2, G3 und G4, mit den Gegenstandsgrößen y1 = y2 = y3 = y4. Diese 4 Gegenstände liegen aber in unterschiedlicher Entfernung von der Linse, haben also unterschiedliche Gegenstandsweiten g1 > g2 > g3 > g4. Wir untersuchen nun, wie die einzelnen Gegenstände an der Linse abgebildet werden. Dazu verwenden wir jeweils einen Parallelstrahl und einen Mittelpunktstrahl.
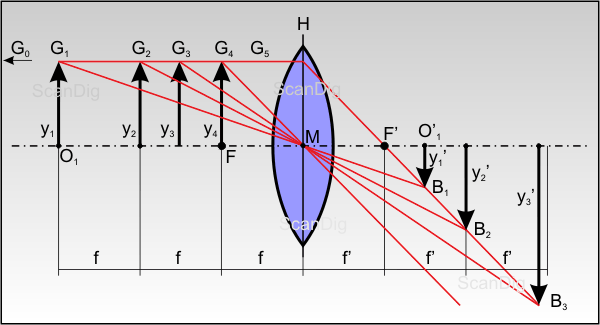
Beginnen wir mit dem Gegenstand G1, der eine Gegenstandsweite von g1 = 3 · f hat, sich also im dreifachen Brennweitenabstand vom Linsenmittelpunkt entfernt befindet. Der von G1 ausgehende Achsenparallelstrahl wird an der Linsen-Hauptebene so gebrochen, dass er durch den bildseitigen Brennpunkt F' verläuft. Der von G1 ausgesandte Mittelpunktstrahl durchdringt die Linse ohne Ablenkung, so dass er den abgelenkten Parallelstrahl im Bildpunkt B1 schneidet. Der Bildpunkt B1 des von der Linse weit entfernten Gegenstandspunkte G1 befindet sich also kurz hinter dem bildseitigen Brennpunkt F', die Bildweite b1 ist also etwas größer als die Brennweite f. Die Bildgröße y1' ist kleiner als die Gegenstandsgröße y1.
Betrachten wir den zweiten Gegenstand G2, dessen Gegenstandsweite g2 = 2 · f ist; er befindet sich also exakt in doppeltem Brennweitenabstand von der Linse. Den zugehörigen Bildpunkt B2 konstruieren wir wieder mit Hilfe eines Parallelstrahles und eines Mittelpunktstrahles. Aus der Zeichnung können wir sofort ablesen, dass die Bildweite b2 der doppelten Brennweite entspricht. Befindet sich der Gegenstandspunkt also in zweifacher Brennweitenentfernung von der Linsenmitte, so befindet sich auch der zugehörige Bildpunkt in zweifacher Brennweitenentfernung auf der Bildseite; es gilt also b2 = g2 = 2f. Für das Abbildungsverhältnis gilt: y2' = y2
Betrachten wir nun den dritten Gegenstand G3, der sich in ungefähr 1,5 facher Brennweitenentfernung vom Linsenmittelpunkt M befindet. Es ist also g3 = 1,5 · f. Die Konstruktion des Bildpunktes B3 mit einem Achsenparallelstrahl und einem Mittelpunktstrahl ergibt für die Bildweite b3 einen Wert größer als der zweifachen Brennweite. Auch erkennen wir aus der Abbildung, dass die Bildgröße y3' größer ist als die Gegenstandsgröße y3, es findet also eine Vergrößerungsabbildung statt.
Die Abbildung des Gegenstandes G4 ist ein Spezialfall, denn dieser befindet sich im Brennpunkt F der Sammellinse. Bei der Konstruktion des Bildpunktes erkennt man, dass der Achsenparallelstrahl und der Mittelpunktstrahl nach der Brechung an der Linse parallel von dieser weglaufen, so dass sie sich nie schneiden. Es entsteht also kein Bildpunkt B4.
Nicht eingezeichnet in der obigen Abbildung ist ein weiterer Spezialfall mit einem Gegenstandspunkt G0, der sich links der Linse in unendlicher Entfernung befindet. Ein von einer Bikonvexlinse unendlich entfernter Gegenstandspunkt sendet nur Parallelstrahlen auf die Linse, die gemäß vorigem Kapitel alle im Brennpunkt F' gesammelt werden. Der zugehörige Bildpunkt B0 liegt also im bildseitigen Brennpunkt F' und hat eine unendlich kleine Größe, also y0' = 0.
Der Vollständigkeit halber sei noch der Fall erwähnt, dass der Gegenstandspunkt G5 innerhalb der Brennweite f liegt. Während bei einem Gegenstandspunkt G4 der Achsenparallelstrahl und der Mittelpunktstrahl parallel von der Linse wegstrahlen, verlaufen beim Gegenstand G5 die beiden Strahlen divergent von der Linse weg. Sie schneiden sich aber auf der Gegenstandsseite links des Gegenstandspunktes. Es entsteht ein aufrechtes, vergrößertes aber virtuelles Bild. Virtuell deshalb, weil man ein solches Bild nicht auf einer Mattscheibe, auf einem Film oder auf einem CCD-Chip auffangen kann. Der Fall G5 hat in der Fotografie keine Bedeutung, findet aber seine Anwendung bei Vergrößerungslupen. Halten wir die oben beschrieben Abbildungsfälle fest:
Ein unendlich weit entfernter Gegenstand G0 wird im bildseitigen Brennpunkt F' der Linse unendlich klein abgebildet. Befindet sich der Gegenstand G1 in größerer Entfernung als der zweifachen Brennweite, so entsteht ein kopfstehendes, verkleinertes Bild B1 rechts des bildseitigen Brennpuntkes F'. Befindet sich der Gegenstand G2 in exakt zweifacher Brennweitenentfernung von der Linse, so entsteht ein gleich großes Bild B2 in zweifacher Brennweiten-Entfernung auf der Bildseite. Befindet sich der Gegenstand G3 zwischen einfacher und zweifacher Brennweite von der Linse entfernt, so entsteht bei der Abbildung ein vergrößertes Bild B3. Befindet sich der Gegenstand G4 im Brennpunkt der Linse, so entsteht auf der Bildseite kein Bildpunkt.
Diese Aussagen im grauen Kasten kann man auch auf einfache Weise zusammenfassen: Ein von der Linse unendlich weit entfernter Gegenstand G0 wird im bildseitigen Brennpunkt F' unendlich klein abgebildet. Je näher der Gegenstand an den Brennpunkt F heranrückt, desto weiter entfernt vom Brennpunkt F' und desto größer wird er abgebildet. Liegt der Gegenstand G4 im Brennpunkt F, so entsteht kein Bild mehr.
Bei Kamera-Objektiven spielt sich die Abbildung im Bereich zwischen G0 und G1 ab. G0 entspricht der Entfernungseinstellung auf unendlich; G1 entspricht der Naheinstellgrenze, die bei Festbrennweitenobjektiven bei ungefähr der 10- bis 20-fachen Brennweite entspricht. Spezielle Makroobjektive schaffen Abbildungsmaßstäbe von 1:1 und größer, liegen also im Bereich zwischen G2 und G3. Damit eine Kamera zwischen unendlich und der Naheinstellgrenze ein scharfes Bild erzeugen kann muss der Kameraauszug zwischen der Brennweite und etwas mehr flexibel sein. Moderne Objektive erreichen dies durch die Verschiebung einer Linsengruppe. Halten wir diesen wichtigen Aspekt bezüglich Kameras fest:
Bei einem Normalobjektiv entspricht der oben beschriebene Fall G0 der Fokusierung auf unendlich; der Fall G1 entspricht der Naheinstellgrenze. Bei einem Makroobjektiv entspricht der Fall G2 einer 1:1-Abbildung, der Fall G3 einer Bildvergrößerung.
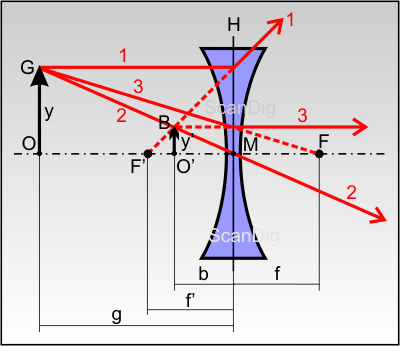
Auch wenn in der Fotografie und in den meisten Fachgebieten der Optik Konkavlinsen nur eine untergeordnete Rolle spielen bzw. nur im Zusammenspiel mit Konvexlinsen ihren Einsatz finden betrachten wir dennoch der Vollständigkeit halber die Bildkonstruktion bei einer Konkavlinse in Abbildung 8. Wir wollen das Bild des Gegenstandes G mit der Gegenstandsgröße y ermitteln. Dazu verwenden wir genauso wie bei Konvexlinsen mindestens 2 der 3 Hauptstrahlen. In der Abbiludng ist als erster Hauptstrahl ein Parallelstrahl eingezeichnet, der parallel zur optischen Achse auf die Linse trifft und dann von dieser so weggebrochen wird, als käme er vom Brennpunkt F' der Linse. Der zweite Hauptstrahl ist der Mittelpunktstrahl, der ohne Ablenkung durch die Linse hindurchtritt. Als dritter Hauptstrahl ist ein Brennpunktstrahl eingezeichnet, der in Richtung Brennpunkt F auf die Linse zuläuft und dann zu einem Parallelstrahl weggebrochen wird. Aus der Zeichnung ist erkennbar, dass sich der Mittelpunktstrahl sowie die rückseitigen Verlängerungen von Parallelstrahl und Brennpunktstrahl im Bildpunkt B schneiden.
Die Lichtstrahlen, die vom Gegenstand G auf die Linse fallen, werden von dieser derart zerstreut, so dass rechts der Linse kein reelles Bild entsteht; man erhält ein diffuses Strahlenbündel, dass sich nicht mehr zu einem einheitlichen Bild zusammensetzt. Bei dem Bildpunkt B auf der linken Seite der Linse handelt es sich um ein virtuelles, aufrecht stehendes Bild; virtuell deshalb, weil es sich nicht mit einer Mattscheibe, einem Film oder einem Sensor erfassen lässt. Die Bildgröße y' ist kleiner als die Gegenstandsgröße y, d.h. die Konkavlinse hat die Wirkung eines Verkleinerungsglases.
Abbildungsmaßstab und Abbildungsgleichung
Bei der Bildkonstruktion von Konvexlinsen und Konkavlinsen im vorigen Kapitel haben wir immer wieder vom Abbildungsmaßstab gesprochen. So wurde zum Beispiel bei der Abbildung des Gegenstandes G2 ein Abbildungsmaßstab von 1:1 erreicht, d.h. die Bildgröße b ist exakt gleich groß wie die Gegenstandsgröße g. Wie ist der Abbildungsmaßstab bei einer Linse definiert?
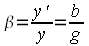
Als Abbildungsmaßstab β bezeichnet man den Quotienten aus der Bildgröße y' und der Gegenstandsgröße y. Aus der Abbildung 6 im vorigen Kapitel kann man mit Hilfe des Strahlensatzes ablesen, dass sich dieser Quotient auch aus den beiden Maßen b (Bildweite) und g (Gegenstandsweite) berechnen lässt. Dieser Sachverhalt ist in nebenstehender Formel 1 mathematisch dargestellt. Ein Abbildungsmaßstab von 1:1 bedeutet, dass Bildgröße und Gegenstandsgröße gleich groß sind, d.h. der Gegenstand wird in Originalgröße abgebildet. In der Fotografie benötigt man für 1:1 Abbildungen spezielle Makroobjektive.
Verkleinerungen werden mit einem Abbildungsmaßstab von 1:x angegeben. Hat man beispielsweise einen Abbildungsmaßstab von 1:10 so wird ein Gegenstand 10 mal kleiner abgebildet als im Original. Eine Landkarte bildet zum Beispiel eine Stadt im Maßstab von 1:10.000 ab, d.h. 1 cm auf der Landkarte entspricht 10.000 cm (=100 m) Stadtgebiet. Normale Objektive führen in der Fotografie immer zu einer Verkleinerung des Gegenstandes, haben also einen Abbildungsmaßstab von zum Beispiel 1:100.
Vergrößerungen werden mit einem Abbildungsmaßstab von x:1 angegeben. Ein Makroobjektiv bildet zum Beispiel einen Gegenstand im Maßstab 2:1 ab, d.h. ein 1 cm großes Insekt wird auf dem Film bzw. auf dem Chip mit einer Größe von 2 cm abgebildet.
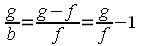
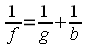
Betrachten wir noch einmal Abbildung 6 im vorigen Kapitel, und zwar die beiden Dreiecke, die vom Brennpunktstrahl 3 auf der Gegenstandsseite erzeugt werden: Mit Hilfe des Strahlensatzes lässt sich aus den Dreiecken FOG und FMS (S = unterer Schnittpunkt des Brennpunktstrahles 3 mit der Hauptebene H) die Formel 2 ablesen. Dividiert man in dieser Gleichung durch g, so erhält man nach entsprechender Umstellung die wichtige Formel 3. Diese Gleichung wird als Abbildungsgleichung oder auch als Linsengleichung bezeichnet. Sie sagt aus, dass der Kehrwert der Brennweite sich aus den Kehrwerten von Bildweite und Gegenstandsweite addiert. Halten wir dieses Ergebnis fest:
Die Abbildungsgleichung für optische Linsen besagt, dass sich der Kehrwert der Brennweite aus der Summe der Kehrwerte von Gegenstandsweite und Bildweite ergibt.
Die obigen Formeln für den Abbildungsmaßstab und die Abbildungsgleichung sind die Grundlage für zahlreiche Berechnungen bei optischen Linsensystemen. So kann zum Beispiel bei Fachkameras aus bekannter Objektivbrennweite und dem maximal möglichen Kamerauszug für eine bestimmte Gegenstandsgröße die resultierende Bildgröße auf dem Film berechnet werden.
| Gegenstands- punkt G |
Gegenstands- weite g |
Bildweite b |
Bildgröße y' |
Abbildungs- maßstab β |
Bildart |
| G0 |
g = ∞ |
b = f |
y' = 0 |
β = 0 |
unendlich klein |
| G1 |
g > 2f |
2f > b > f |
y' < y |
β < 1 |
reel, kopfstehend |
| G2 |
g = 2f |
b = 2f |
y' = y |
β = 1 |
reel, kopfstehend |
| G3 |
2f > g > f |
b > 2f |
y' > y |
β > 1 |
reel, kopfstehend |
| G4 |
g = f |
b = ∞ |
y' = ∞ |
β = ∞ |
kein Bild |
| G5 |
g < f |
b < 0 |
y' > y |
β > 1 |
virtuell, aufrecht |
Im vorigen Kapitel haben wir mit Hilfe der Abbildung 7 für unterschiedliche Gegenstandspunkte G0 bis G5 bei gleicher Gegenstandsgröße y untersucht, welche Bildweite b und welche Bildgröße y' sich durch die Abbildung an einer Konvexlinse ergibt. Diese Ergebnisse sind in obiger Tabelle nochmals zusammengefasst. Außerdem ist der zu jedem Fall zugehörige Abbildungsmaßstab β mit angegeben. Anhand des jeweils resultierenden Abbildungsmaßstabes erkennen wir, dass nur die Fälle G1 bis G3 für die Praxis relevant sind. Die praktische Einstellung auf unendlich (Fall G0) entspricht in Wirklichkeit dem Fall G1 mit einer sehr großen, aber endlichen Gegenstandsweite g.
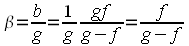
Die obige Formel 1 für den Abbildungsmaßstab spiegelt die bekannte Begebenheit wider, dass der Abbildungsmaßstab sich aus dem Verhältnis von Bildgröße zu Gegenstandsgröße errechnet. In der Fotografie gibt es jedoch noch eine weitere wichtige Begebenheit, die jeder Fotograf aus dem Alltag kennt, nämlich: Um den Abbildungsmaßstab zu vergrößern nimmt man einfach ein Objektiv mit größerer Brennweite. Diese Begebenheit lässt sich leicht aus den Formeln 1 und 3 herleiten. Löst man die Formel 3 nach der Bildweite b auf, so erhält man b = g · f / (g - f). Setzt man dies in Formel 1 ein, so erhält man den Abbildungsmaßstab β in Abhängigkeit von der Brennweite f und der Gegenstandsweite g, siehe Formel 4.
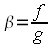
Nehmen wir an, dass wir mit einem 50 mm Objektiv einen Baum fotografieren, der sich in 10 m Entfernung befindet. Dann berechnet sich gemäß Formel 4 der Abbildungsmaßstab zu β = 0,05 / (10,0 - 0,05) = 0,005025. Für solche typischen Aufnahmeszenarien mit g >> f kann man die Formel 4 derart vereinfachen, dass sich der Abbildungsmaßstab als Quotient aus Brennweite und Gegenstandsweite ergibt, also β = f / g, siehe Formel 5. Im Beispiel erhält man dann für den Abbdildungsmaßstab β = 0,05 / 10,0 = 0,005.
Befindet sich der zu fotografierende Gegenstand in großer Entfernung relativ zur Brennweite des Objektives, dann ist der Abbildungsmaßstab proportional zur Brennweite des Objektives und antiproportional zur Gegenstandsweite des zu fotografierenden Objektes.
Viel wichtiger als die Berechnung des Abbildungsmaßstabes aus Brennweite f und Gegenstandsweite g ist jedoch die Erkenntnis, dass der Abbildungsmaßstab β proportional zur Brennweite f und antiproportional zur Gegenstandsweite g ist. Verdoppelt man also die Brennweite so verdoppelt man auch das Abbildungsverhältnis bei einem Objekt, das in einer bestimmten Entfernung g zur Kamera steht. Umgekehrt halbiert sich der Abbildungsmaßstab, wenn man um die Hälfte näher ans Objekt heranrückt, die Gegenstandsweite also halbiert.
Diesen Sachverhalt veranschaulichen wir in obiger Abbildung 9: Ein Gegenstand G1 befindet sich im Abstand g = 5f, also in 5-fachem Brennweitenabstand von der Linse. Hat die Linse die Brennweite f, so entsteht ein Bildpunkt B1 nahe bei der Linse. Verdoppelt man die Brennweite der Linse auf 2f, so entsteht ein proportional größeres Bild B2 mit der Bildgröße y2'. Erhöht man die Brennweite der Linse weiter auf 3f, so entsteht der Bildpunkt B3 mit der Bildgröße y3'. Die Proportionalität ergibt sich aus der Zeichnung dadurch, dass der die Gegenstandsweite g konstant bleibt und sich der Mittelpunktstrahl durch die unterschiedlichen Brennweiten nicht ändert. Lediglich der von G1 ausgehende Paralellstrahl wird durch die unterschiedlichen Brennweiten mehr oder weniger stark gebrochen.
Brechung von Lichststrahlen an dicken Linsen
In den vorigen Kapiteln haben wir die Gesetzmäßigkeiten für die Brechung von Lichtstrahlen an optischen Linsen gelernt. Zur Konstruktion des Bildes haben wir sowohl bei Konvexlinsen als auch bei Konkavlinsen 3 Hauptstrahlen verwendet, von denen der Mittelpunktstrahl ohne Richtungsänderung durch die Linse hindurchlief während Parallelstrahl und Brennpunktstrahl an der Hauptebene in der Mitte der Linse gebrochen wurden. In den vorigen Kapiteln haben wir dünne Linsen vorausgesetzt bzw. wir haben die Linsendicke vernachlässigt, weil wir nur die optischen Eigenschaften von Linsen kennenlernen und keine detaillierten Linsenberechnungen machen wollten. Damit haben wir eine starke Vereinfachung gemacht, die uns das Leben erheblich vereinfacht.
Eine dünne Linse zeichnet sich dadurch aus, dass ihre Dicke gegenüber den Brennweiten klein ist.
In der Praxis hat natürlich jede Linse eine gewisse Dicke, und nicht selten kommen in optischen Instrumenten richtig dicke Linsen zum Einsatz. Für die einfache Bildkonstruktion und für einfache Berechnungen, wie wir sie in den vorigen Kapiteln gemacht haben, genügt die Betrachtung von dünnen Linsen völlig. Um ganze Linsensysteme zu berechnen, die Abbildungseigenschaften von Objektiven exakt nachzuvollziehen und gar Linsengruppen zu optimieren muss jede einzelne Linse natürlich genau berechnet und das Bild im Detail konstruiert werden. Wir wollen hier keine Objektive bzw. Linsensysteme konstruieren bzw. berechnen, dennoch werfen wir im Folgenden einen Blick auf die Eigenschaften von dicken Linsen und deren Bildkonstruktion.
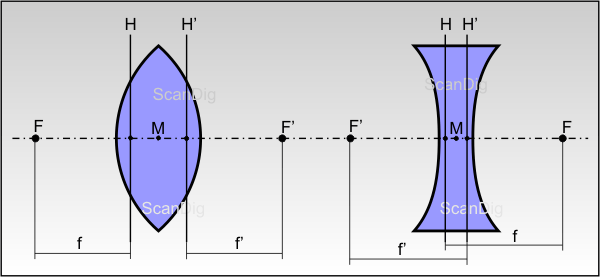
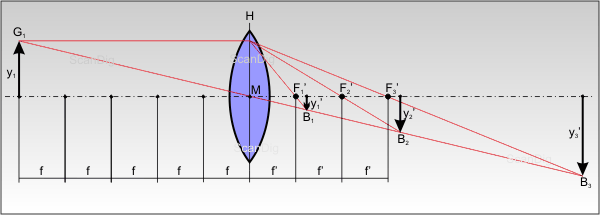
Abbildung 10 zeigt links eine dicke Konvexlinse und rechts eine dicke Konkavlinse. Beide Linsen bezeichnet man als dick, da die Linsendicke gerade mal halb so groß wie die Linsenbrennweite ist. Dicke Linsen unterscheiden sich von dünnen Linsen dadurch, dass sie nicht eine einzige Hauptebene in der Linsenmitte sondern eine gegenstandsseitige Hauptebene H und eine bildseitige Hauptebene H' haben. Trägt man von den bekannten und leicht messbaren Brennpunkten der Linse F und F' die jweiligen Brennweiten f und f' auf der optischen Achse ab, so findet man zwei Hauptpunkte, durch die senkrecht zur optischen Achse und im Linsenschnitt die jeweiligen Hauptebenen H und H' verlaufen.
Bei der Konkavlinse scheinen im Bild die Brennpunkte F und F' vertauscht zu sein. In der Zeichnung ist jedoch kein Fehler vorhanden. Betrachten wir dazu Abbildung 8 weiter oben: Der von links kommende Brennpunktstrahl 3 findet in der Verlängerung rechts der Linse im Brennpunkt F sein Ziel, wird aber durch die Linse in einen Parallelstrahl abgelenkt. Der Parallelstrahl 1 wird von der Konkavlinse so abgelenkt als käme er vom virtuellen Brennpunkt F'. Die Tatsache, dass bei einer Konkavlinse der gegenstandsseitige Brennpunkt F hinter der Linse (rechts der Linse) und der bildseitige Brennpunkt F' vor der Linse (links der Linse) liegt, ist damit zu erklären, dass eine Konkavlinse vor der Linse (links der Linse) ein virtuelles Bild erzeugt, während von einer Konvexlinse hinter der Linse (rechts der Linse) ein reelles Bild erzeugt wird.
Welche Auswirkung hat die Linsendicke auf die Abbildung eines Bildes? Betrachten wir dazu exemplarisch die Bildkonstruktion an einer dicken Konvexlinse in Abbildung 11. Unser Gegenstand G befindet sich im Abstand g (Gegenstandsweite) von der Hauptebene H der Linse. Zur Bildkonstruktion betrachten wir wieder den Verlauf von 3 Hauptstrahlen. Der erste Hauptstrahl ist ein Parallelstrahl; dieser läuft durch die erste Hauptachse hindurch und wird erst an der Hauptachse H' so gebrochen, dass er durch den bildseitigen Brennpunkt F' verläuft. Der zweite Hauptstrahl ist ein Mittelpunktstrahl; dieser wird durch die zweimalige Ablenkung an den Hauptebenen H und H' so gebrochen, dass eine Parallelverschiebung des ursprünglichen Strahles stattfindet. Der dritte Hauptstrahl ist ein Brennpunktstrahl, der durch den gegenstandsseitigen Brennpunkt F verläuft, bis er auf die Linse trifft und dort an der ersten Hauptebene in einen Parallelstrahl abgelenkt wird. Die 3 abgelenkten Hauptstrahlen treffen sich im Bildpunkt B wieder. Die Bildweite b wird als Abstand von der Hauptebene H' angegeben. Halten wir dies fest:
Bei einer dicken Konvexlinse wird ein Parallelstrahl an der bildseitigen Hauptebene H' in einen Brennpunktstrahl abgelenkt, ein Mittelpunktstrahl erfährt eine Parallelverschiebung, und ein Brennpunktstrahl wird an der gegenstandsseitigen Hauptebene H in einen Parallelstrahl abgelenkt.
Wir sehen, dass die Bildkonstruktion bei einer dicken Linse etwas komplizierter ist als bei einer dünnen Linse; die Gesetzmäßigkeiten bleiben aber gleich. Auch die optischen Eigenschaften von Linsen bleiben gleich. So erkennen wir im obigen Bild, dass die Gegenstandsweite g im Bereich der ein- und zweifachen Brennweite liegt; die Bildgröße y' ist demnach größer als die Gegenstandsgröße y (Fall G3 im vorigen Kapitel).
Auch erkennen wir aus der obigen Abbildung leicht, wie sich die Abbildungseigenschaften von dünnen Linsen aus denen von dicken Linsen ableiten lassen: Bei einer dünnen Linse fallen die Hauptebenen H und H' zusammen, so dass der Parallelstrahl 1 und der Brennpunktstrahl 3 an der gemeinsamen Hauptebene abgelenkt werden und dass der Mittelpunktstrahl 2 keine Parallelverschiebung mehr erfährt sondern einfach durch die Linse hindurchdringt.
Zum Abschluss dieses Kapitels sei noch einmal erwähnt, dass Fotografen, die sich für Abbildungseigenschaften einzelner Linsen, Linsengruppen oder ganzer Objektive interessieren, mit der vereinfachten Annahme von dünnen Linsen arbeiten. Ja sogar ganze Objektive, die zum Teil aus 10 bis 20 einzelnen Linsen bestehen, lassen sich wie eine einzelne Linse mit einer einzigen Hauptebene behandeln, wenn es auf keine detaillierten Berechnungen sondern nur um Abbildungsprinzipien oder Abbildungsfehler ankommt.
Berechnung der Brennweite von Linsen
Der Brennpunkt einer Linse lässt sich mit einem praktischen Experiment ganz leicht ermitteln: Man lässt eine Lichtquelle parallel zur optischen Achse von einer Seite aus die Linse durchstrahlen und verschiebt im Bildraum eine Mattscheibe so hin und her bis der resultierende Lichtfleck am kleinsten wird. Ist dies der Fall befindet sich die Mattscheibe im Brennpunkt, das parallel einfallende Licht wird in diesem Punkt fokusiert.
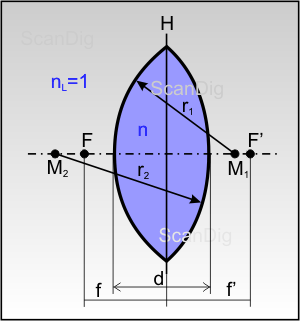
Im Normalfall kennt man die Brennweite einer Linse, denn die Brennweite ist schließlich die wichtigste Eigenschaft einer optischen Linse. Bei der Entwicklung bzw. bei der Konstruktion einer optischen Linse wird die Brennweite exakt berechnet. In Abbildung 12 sind die wichtigen Parameter zur Berechnung einer Bikonvexlinse eingezeichnet: Die linke Linsenoberfläche hat einen Krümmungsradius r1 mit dem Krümmungsmittelpunkt M1. Die rechte Linsenoberfläche hat den Krümmungsradius r2 mit dem Krümmungszentrum M2. Die Dicke der Linse wird mit d bezeichnet. Das Linsenmaterial hat die Brechzahl n, während die Brechzahl des umgebenden Materials (Luft) nL = 1 ist. Die Parameter r1, r2, d und n müssen bekannt sein, um die Brennweite der Linse berechnen zu können. Ist dies der Fall wird die Brennweite gemäß der Formel 6 berechnet. In dieser Formel wird zunächst die Brechkraft der Linse berechnet; die Brennweite ergibt sich als Kehrwert 1/f. Die Krümmungsradien müssen jeweils als positive Werte in die Formel eingesetzt werden.
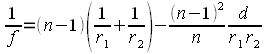
Beispiel 1: Unsere dicke Linse habe als Krümmungsradien r1 = 100mm = 0,1m und r2 = 200mm = 0,2m. Die Linsendicke sei 7cm, also d = 0,07m. Der Brechungsindex des Linsenmaterials sei n=1,5. Dann berechnet sich gemäß Formel 6 der Kehrwert der Brennweite als 1/f = 7,5 - 0,6 = 6,9. Daraus ergibt sich als Brennweite für die Linse f=0,14m. Bei der Anwendung der Formel fließen die Radien also positive Zahlen in die Berechnung ein (keine Vorzeichenumkehr bei r1 weil der Vektor nach links zeigt).
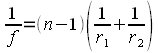
Wie berechnet sich die Brennweite bei einer dünnen Linse? Eine dünne optische Linse ist dadurch definiert, dass die Linsendicke d viel kleiner ist als die Brennweite f bzw. dass die Linsendicke viel kleiner ist als die Differenz der beiden Radien r2-r1. Unter dieser Voraussetzung lässt sich der rechte Summand der Formel 6 vernachlässigen, so dass sich als vereinfachte Gleichung für die Brennweitenberechnung die nebenstehende Formel 7 ergibt.
Beispiel 2: Unsere Linse aus Beispiel 1 habe eine Dicke von nur 7mm, also d=0,007m. Die Krümmungsradien sowie der Brechungsindex bleiben gleich. Gemäß der ausführlichen Formel 6 zur Brennweitenberechnung ergibt sich als Brechkraft der Linse 1/f = 7,5 - 0,06 = 7,44. Mit der vereinfachten Formel 7 für dünne Linsen ergibt sich als Brechkraft 1/f = 7,5. Daraus ergibt sich eine Brennweite von f=13cm. Anhand dieses Beispieles erkennt man, dass der zweite Summand in Formel 6 bei dünnen Linsen tatsächlich vernachlässigbar ist, so dass die vereinfachte Formel 7 angwendet werden kann.
Die Brennweite f einer Linse lässt sich aus den Krümmungsradien r1 und r2 der Linsenoberflächen sowie der Linsendicke d und dem Brechungsindex n des Linsenmaterials berechnen.
Für die beiden Brennweiten f und f' gilt stets f=f'. Die Formeln zur Brennweitenberechnung lassen sich bei der Linsenkonstruktion natürlich umgekehrt nutzen, um bei einer bestimmten Nominal-Brennweite für die Linse die Krümmungsradien entsprechend auszulegen.
Der Brechwert einer Linse
Im Kapitel Brennweitenberechnung haben wir gezeigt, wie man für eine optische Linse aus den Krümmungsradien der Linse r1 und r2 sowie der Linsendicke d und dem Brechungsindex n die Brennweite f der Linse berechnet. Dabei haben wir Gleichungen in der Form 1/f angegeben, also zuerst den Kehrwert der Brennweite berechnet.
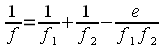
Die Formel 6 zur Berechnung der Brennweite einer dicken Linse ist schon eine ordentlich lange Gleichung. Der Ausdruck wird noch viel länger, wenn man zwei konvexe Linsen in Reihe schaltet. Die nebenstehende Formel 8 zeigt, wie man die Gesamtbrennweite eines Linsensystems, das aus zwei nebeneinander liegenden Konvexlinsen besteht, berechnet; dabei ist e der Abstand der beiden Linsen. Es addieren sich die Kehrwerte der Einzelbrennweiten, korrigiert um einen vom Linsenabstand e abhängigen Korrekturterm.
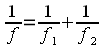
Ist der Abstand e der beiden Linsen klein gegenüber den Einzelbrennweiten f1 und f2, dann kann der Korrekturterm in Formel 8 vernachlässigt werden und man erhält die einfache Formel 9 zur Berechnung der Gesamtbrennweite. Diese vereinfachte Formel hat große Bedeutung in der Praxis, denn oftmals werden Linsen in kleinem Abstand e direkt hintereinander angebracht. Ein einfaches Beispiel aus der Fotopraxis ist das Anbringen einer Vorsatzlinse am Objektiv.
Die Berechnung der Brennweite einer einzelnen Linse oder die Berechnung der Gesamtbrennweite eines Linsensystems gestaltet sich als einfacher, wenn man wie in den obigen Formeln gezeigt mit dem Kehrwert der Brennweite rechnet. Die einfachen Formeln 8 oder 9 würden um einiges komplizierter, wenn man sie nach der Brennweite auflösen würde, und würden die Zeilenbreite gar sprengen, wenn man die jeweilige Formel 6 für die Brennweite noch einsetzen würde.
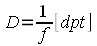
Noch einfacher werden die Berechnungen wenn man anstatt mit der Brennweite mit dem sogenannten Brechwert rechnet. Die Brechkraft einer Linse gibt an, wie stark Licht von einer Linse gebrochen wird. Der Brechwert D ist als Kehrwert der Brennweite f definiert. Während die Brennweite in Metern angegeben wird, verwendet man für den Brechwert die Einheit Dioptrie, abgekürzt dpt. Bei Konvexlinsen (Sammellinsen) wird die Brechkraft als positive Dioptrie-Zahl angegeben, bei Konkavlinsen (Zerstreuungslinsen) als negativer Wert.
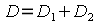
Ersetzen wir in Formel 9 die Brennweiten durch die jeweiligen Brechwerte so ergibt sich die ganz einfache Formel 11: D = D1 + D2. Demnach addieren sich die Brechwerte in einem Linsensystem einfach, falls die Distanz der beiden Linsen e klein gegenüber den Brennweiten ist. Ist die Distanz e zwischen den beiden Linsen nicht vernachlässigbar kommt in Formel 11 eben noch ein einfacher Korrekturterm -e · D1 · D2 hinzu. Die Gleichung bleibt aber immer noch anschaulich und handhabbar. Alleine anhand dieser Formel kann man leicht einsehen, dass man sich bei optischen Berechnungen erheblich leichter tut, wenn man anstatt mit der Brennweite f mit dem Brechwert D rechnet.
Der Brechwert D einer Linse gibt an, wie stark Licht von der Linse gebrochen wird. Er berechnet sich aus dem Kehrwert der Brennweite f und wird in der Einheit Dioptrie [dpt] angegeben.
Um uns ein anschauliches Bild vom Brechwert einer Linse zu machen, werfen wir einen Blick auf die Abbildung 4 ganz oben und auf die nachfolgende Tabelle. Eine Konvexlinse bricht parallel zur optischen Achse einfallende Lichtstrahlen so, dass sie im Brennpunkt gesammelt werden. Je näher der Brennpunkt an der Linse ist, also je kleiner die Brennweite ist, desto stärker werden die Lichtstrahlen gebrochen, desto stärker ist also der Brechwert D der Linse.
Aus der Tabelle kann man ablesen, dass ein 100 mm Objektiv einen Brechwert von 10 Dioptrien hat. Bei einem Weitwinkelobjektiv mit 20 mm Brennweite liegt der Brennpunkt näher am Linsensystem, das Licht wird stärker gebrochen; die Linse hat einen Brechwert von 50 dpt. Je länger die Brennweite einer Linse ist desto weniger wird das Licht abgelenkt um im Brennpunkt gesammelt zu werden. Der Brechwert einer Sammellinse mit 1000 mm Brennweite beträgt genau eine Dioptrie. Geht die Brennweite gegen unendlich dann entspricht die Linse einer ebenen Glasplatte; das Licht wird nicht mehr gebrochen, der zugehörige Brechwert ist 0. Bei Zerstreuungslinsen wird die Brennnweite und damit auch der Brechwert in negativen Zahlenwerten angegeben.
| Linsenart |
Brennweite f |
Brechwert D |
| Sammellinse |
20 mm = 0,02 m |
50 dpt |
| Sammellinse |
100 mm = 0,1 m |
10 dpt |
| Sammellinse |
500 mm = 0,5 m |
2 dpt |
| Sammellinse |
1000 mm = 1 m |
1 dpt |
| Sammellinse |
100 m |
0,01 dpt |
| ebene Glasplatte |
∞ |
0 |
| Zerstreuungslinse |
-500 mm = -0,5 m |
-2 dpt |
| Zerstreuungslinse |
-100 mm = -0,1 m |
-10 dpt |
Ein einfaches Beispiel für die Addition von Brechwerten ist das Anbringen einer Nahlinse an einem Objektiv, um mit einem Normalobjektiv Makroaufnahmen zu machen. Nehmen wir ein Festbrennweitenobjektiv mit 50 mm Brennweite; das entspricht einem Brechwert von 20 dpt. Schrauben wir vor dieses Objektiv eine Nahlinse mit +5 Dioptrien so ergibt sich gemäß Formel 11 die Gesamtbrechkraft D = 20 + 5 = 25 dpt. Das System aus Festbrennweitenobjektiv und Nahlinse hat die neue Brennweite f = 1/25 dpt = 40 mm. Nahlinsen lassen sich (fast) beliebig miteinander verkitten. Setzt man vor das 50mm Objektiv zwei Nahlinsen mit jeweils 5 Dioptrien Brechkraft, so ergibt sich die Gesamtbrechkraft D = 20 + 5 + 5 = 30 dpt. Das Objektiv mit ursprünglich 50 mm Brennweite hat dann nur noch 33 mm Brennweite.
Eine Nahlinse funktioniert also so, dass sie die Gesamtbrechkraft des Systems aus Objektiv und Nahlinse erhöht, so dass sich die Gesamtbrennweite verkleinert. Da der Abstand zwischen Objektiv und Kamera gleich bleibt kann man näher an den zu fotografierenden Gegenstand ran, und der Abbildungsmaßstab vergrößert sich, so dass man ein größeres Bild erhält.
Zurück zum Inhaltsverzeichnis Grundlagen der Fotografie
|